You’re probably familiar with the concept of compounding returns. But you may not be familiar with all the ways of looking at it. Especially when teaching young people about this important idea, it’s helpful to have a few different examples at the ready. Here are some suggestions.
Part A: The basics
Compounding is the idea that when you invest money and it earns a return, that return then earns money, and that return earns money, and on and on. For example, if you invest $100 and it earns a 10% return, at the end of the year, you’ll have $110. The next year, assuming another 10% return, you won’t just earn another $10; you’ll earn $11. That’s because your original $100 earned 10% and so did the $1 you earned the first year. Unto itself, that explanation probably doesn’t sound too exciting, so you have to bring it to life.
One way to do that is to make a distinction between linear growth and exponential growth. For example, if you stuffed $100 under your mattress every month and did that for 50 years, you’d end up with $60,000 (and a very lumpy mattress).
That’s a linear way to build wealth. The money grows by the same amount every month, with $100 turning into $200, and then $300, and then $400, etc.
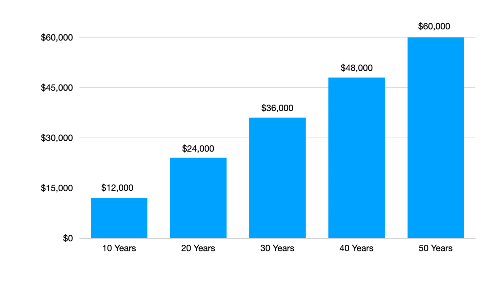
But now let’s do something more productive with the money. Let’s invest it. And let’s assume we’re able to generate an average annual return of 10%. That money won’t grow linearly; it’ll grow exponentially. And what a difference that makes. Fifty years down the road, your $60,000 will have grown to $1,470,000 million! (All of the examples used in this article were generated with this calculator, which assumes annual compounding.)
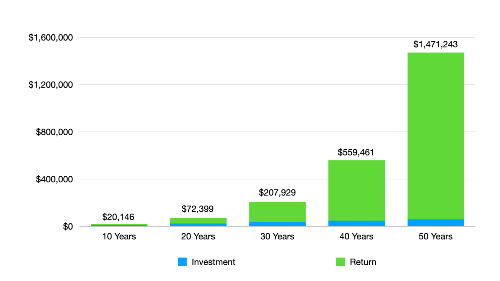
The numbers represented by the blue portions of each bar are the same as in the first chart — $12,000 after 10 years, $24,000 after 20 years, etc. But the scale has changed to make room for all of the gains generated by the 10% average annual return.
One of the interesting things that’s evident from the second chart is that in the early years it doesn’t look like all that much is happening. After 10 years, for example, where you can barely see the $12,000 you would have invested, that money would have earned about $8,100. That’s nice, but not super exciting. Well, now look at the 30-year mark. By then, you would have invested $36,000, but it would have turned into about $208,000. Your earnings would far exceed the amount you invested. And when you look at the 50-year mark, your $60,000 would have generated a return of more than $1.4 million. That’s incredible!
Think of it this way. In one sense, one dollar turning into two dollars is the same thing as $500,000 turning into $1 million. Both figures doubled. But of course, in another very important sense, it’s not at all the same thing. You’d far rather have $500,000 that turns into $1 million than one dollar turning into two dollars. That means — you guessed it — you have to get this multiplying process started as early as possible.
Part B: The importance of starting early
Imagine two 20-year-olds: Early Ed and Later Larry. Ed’s a go-getter. He follows our example by starting to invest $100 per month right away and continuing for 50 years. By then, his $60,000 will have turned into more than $1,470,000.
Larry, on the other hand, figures he’s young. He can start doing all that boring adult stuff, like investing, later. For now, he has things he wants to buy and trips he wants to take. So, he waits 10 years longer than Ed to begin investing. Assuming the same 10% average annual rate of return, after 40 years, Larry ends up with about $560,000 — more than $900,000 less than Ed!
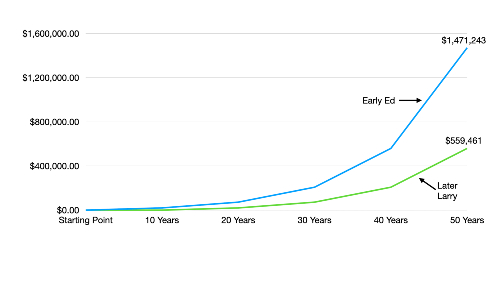
That’s quite a penalty for waiting.
Part C: Did I mention that it’s important to start early?
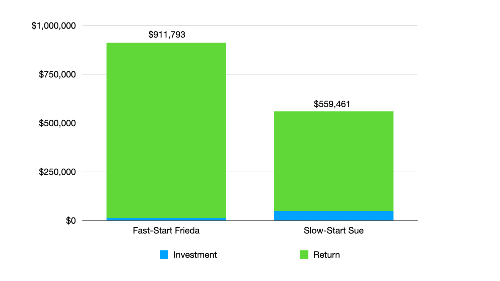
Imagine two other 20-year-olds: Fast-Start Frieda and Slow-Start Sue. Just like Early Ed, Frieda begins investing $100 per month at age 20, and she generates an average annual return of 10%. But after 10 years, she runs into some difficulties that prevent her from investing another dime. She keeps her portfolio invested, but she isn’t able to add to it anymore.
Like Later Larry, Sue waits 10 years to start investing. Then, at age 30, she reliably invests $100 per month for the next 40 years and she, too, generates an average annual return of 10%.
How do their ending portfolios stack up? Frieda, who invested a total of just $12,000, ends up with about $912,000. Sue, who invested four times more money — a total of $48,000 — ends up with just $560,000. That, too, is remarkable, isn’t it? And once again, it shows the importance of starting early.
Part D: Oh, and starting early is really important
Here’s one final way of looking at the power of compounding. Let’s say a new college grad begins a job paying $40,000. She receives a 3% annual raise, contributes 10% of her salary to her 401(k) each year, and earns an average annual return of 10%. In 50 years, her account will total $6.8 million. Nice.
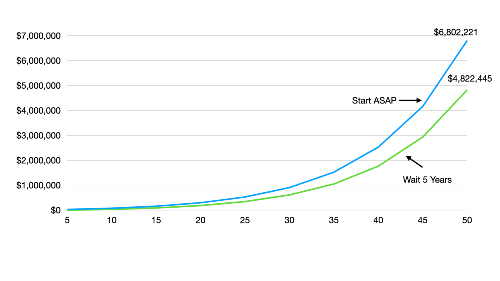
But what if we take away just her first five years of investing? Her total would drop to $4.8 million. That’s still a sizable sum, but think about this: investing a portion of her salary during the first five years of her career — a time when her salary was at its lowest — ends up being worth an incredible $2 million. That’s 29% of her eventual total retirement portfolio. Amazing!
No matter how old you are, the same general principle applies: the earlier you start investing, the better. But the younger you are, the more impact an early start will have. So, if you have a young person in your life, talk to them about the power of compounding. They may not have a lot of money right now, but they have a valuable asset many older people wish they had more of. They have time.
What young people do you need to share this with?









